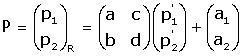Sistemas de referencia. Una referencia R en la recta, plano, espacio ... consta de un punto O y de una base del espacio vectorial asociado.

El punto 0 representa el origen de coordenadas, mientras que los vectores de la base determinan las direcciones de los ejes de proyección.

El ejemplo más habitual es la referencia cartesiana en el plano (o en el espacio):

Ejemplo. Referencia canónica en el plano.

En este caso,. O es un punto cualquiera del plano, y 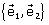son un par de vectores (normalmente, se tomam ortogonales y unitarios), que forman base de R2. Una vez fijada la referencia, cada punto P está caracterizado por sus coordenadas y viceversa. P = (3,2)R (las coordenadas de P en la referencia R son (3,2)) significa que

Observad la equivalencia entre:
      1.- proyectar el punto P sobre los ejes y medir sus proyecciones, y
      2.- obtener el vector OP como combinación lineal de los vectores de la base.

En general, 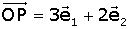si P=(p₁, p₂), o bien
si trabajamos en Rⁿ.

Las coordenadas de un vector son las de su punto extremo cuando el vector está anclado en el origen.

Fijaos en que el origen de coordenadas no influye en las coordenadas de un vector, y que éstas dependen solamente de la base.

Se habla de las coordenadas de un vector respecto de una base B, y no respecto de una referencia R.

Existen otros tipos de coordenadas que no esdudiaremos este curso, pero sí más adelante (Por ejemplo, las coordenadas polares )

Problema. Si y son dos referencias del plano, y el punto P tiene coordenadas en la primera referencia, ¿cuáles son las coordenadas de P en la segunda referencia ?

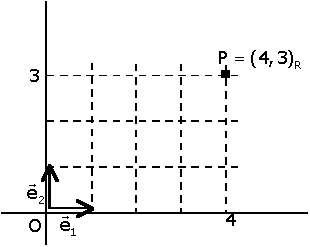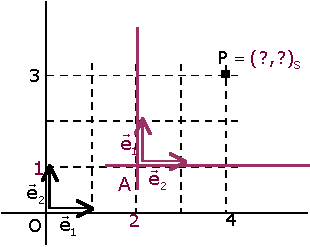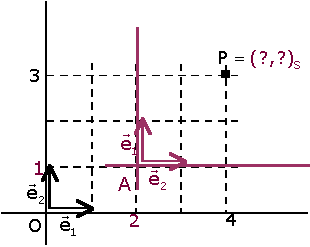
Problema.     Sea una referencia en el plano (la referencia inicial o canónica), y P un punto de coordenadas (3,3)R. Introducimos una nueva referencia (ejes iguales, origen diferente) con A=(2,1)R. ¿Cuáles son las coordenadas de P en la referencia S?
Solución. Se observa que les proyecciones de P sobre los nuevos ejes se obtienen restando las proyecciones de P y A sobre los ejes de la referencia inicial. Por tanto,

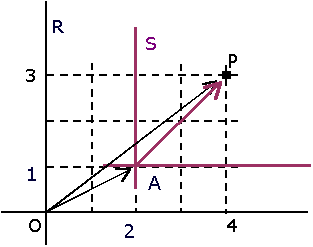
Alternativamente, podemos observar que que escrito en las coordenadas respecto a la base resulta

En general, para un punto P del plano, (espacio,...) y dos referencias y se satisface:

donde (p₁,p₂,...) son las coordenads de P en la referencia inicial R
(p'₁,p'₂,...) son las coordenadas de P en la nueva referencia S, y
(a₁,a₂,...) son las coordenadas del nuevo origen A en la referencia inicial R. 3.3 Cambio de ejes (o de base). A continuación se estudia cómo varían las coordenadas de un punto en función de los ejes de referencia escogidos, cuando el origen se mantiene fijo .

Las direcciones y unidades de medida de los ejes vienen determinados únicamente por los vectores de la base. De aquí que se hable indistintamente de cambio de ejes o de cambio de base .

Empezamos con un ejemplo.

Problema. Se consideran las referencias y donde y 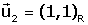. Si P tiene coordenadas en la referencia R, ¿cuáles son sus coordenadas 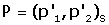en la referencia S?
Solución gráfica. Si Q y P son las proyecciones de P sobre los nuevos ejes de coordenadas, entonces p'1 es la longitud del segmento 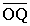p'2 es la longitud del segmento.

Solución algebraica. Se considera la matriz M que tiene por columnas las coordenadas de los vectores 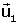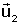en la referencia R, y se calcula su inversa M-1.
Las coordenadas de P en la referencia S se obtienen efectuando el producto de M-1 por las coordenadas

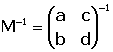En general, si y son dos referencias en el plano y se conocen las coordenadas en la referencia R de los vectores de S, y entonces la matriz se llama matriz del cambio de base (o de ejes) de R a S, y satisface parar cualquier punto .

• La matriz M^-1 es la única que satisface la propiedad anterior.
• El proceso descrito es absolutamente general, y sirve también para referencias con 3 o más vectores (espacio, ...)

(sigue el ejemplo anterior)   Teniendo en cuenta que las coordenadas de P en la referencia S son los coeficientes p'1, p'2 utilizados en la combinación lineal Por tanto, p'1, p'2 son las soluciones del sistema que no son otros que

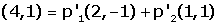
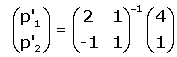
En general, la combinación lineal a considerar es que matricialmente se escribe en la forma

o, alternativamente

Pero también se puede plantear el problema inverso:
conocidas las coordenadas de P en la referencia S, , determinar las coordenadas de P en la referencia R, .

Observad (final del apartado anterior) que la matriz M resuelve el problema planteado.
M es la matriz del cambio de S a R.

Problema. Se consideran las referencias y donde , y 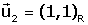. Si las coordenadas de P son en la referencia R, ¿cuáles son sus coordenadas 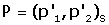en la referencia S?

Solución. Introducimos una referencia auxiliar . Les coordenadas de P en la referencia T son (cambio de origen): Efectuando ahora un cambio de ejes de T a S se obtiene:

En general, si y son las dos referencias en el plano y se conocen las coordenadas en la referencia R de los vectores de S, y y las del origen , entonces

El proceso descrito es totalmente general y sirve tambien para las referencias con 3 o más vectores (espacio, ...)