3.1 El problema del canvi de referència.
Sistemes de referència.
Una referència R a la recta, pla, espai ... consta
d'un punt O i d'una base
 de l'espai vectorial associat.
de l'espai vectorial associat.
El punt O representa l'origen de coordenades, mentre que els vectors de la base
determinen les direccions dels eixos de projecció.
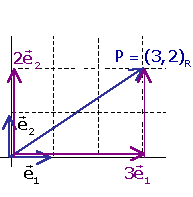
L'exemple més habitual és la referència cartessiana al pla (o a l'espai):
Observeu l'equivalència entre:
1.- projectar el punt P sobre els eixos i mesurar-ne les projeccions, i
2.- obtenir el vector OP com a combinació lineal dels de la base.
En general, 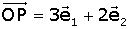 si P=(p1, p2), o bé
si P=(p1, p2), o bé
 si treballem a Rn.
si treballem a Rn.
Les coordenades d'un vector són les del seu punt extrem quan el vector està ancorat a l'origen.
Noteu que l'origen de coordenades no influeix en les coordenades d'un vector, i que aquestes
depenen només de la base.
Es parla de les coordenades d'un vector respecte d'una base B,
 i no respecte d'una referència R.
i no respecte d'una referència R.
Hi ha d'altres tipus de coordenades que no
esdudiarem aquest curs, però sí més endavant
(Per exemple, les coordenades polars
 )
)
Canvi de referència.
Sistemes de referència diferents assignen coordenades diferents a un mateix punt del pla (espai, ...).

|
|
Problema.
Si  i i
 són
dues referències del pla, i el punt P té coordenades són
dues referències del pla, i el punt P té coordenades  en la primera referència, quines són les coordenades de P
en la segona referència
en la primera referència, quines són les coordenades de P
en la segona referència
 ? ?
|
Un canvi de referència es pot desglossar en dues operacions diferents: canvi d'origen i canvi d'eixos.
¿
 .
.
 són un parell de vectors
(normalment, es prenen ortogonals i unitaris), que formen base de R2.
són un parell de vectors
(normalment, es prenen ortogonals i unitaris), que formen base de R2.
 de l'espai vectorial associat.
de l'espai vectorial associat.
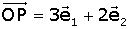
 si treballem a Rn.
si treballem a Rn.
 i no respecte d'una referència R.
i no respecte d'una referència R.
 )
)

 són
dues referències del pla, i el punt P té coordenades
són
dues referències del pla, i el punt P té coordenades  en la primera referència, quines són les coordenades de P
en la segona referència
en la primera referència, quines són les coordenades de P
en la segona referència
 ?
?