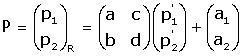3.4 Canvi global de referència.
Tractem ara la situació més general, en què la referència original
 i la nova referència
i la nova referència
 no mantenen cap element, ni
origen ni eixos, en comú.
no mantenen cap element, ni
origen ni eixos, en comú.
Aquest cas es pot reduïr a una seqüència de dos ja vistos:
1. Canvi d'origen (de O a A).
2. Canvi de base (de  a
a
 .
.
Nota: l'ordre no és rellevant.
Descomposició en dos canvis successius.
Problema. Es considera les referències
 i i
 on on
 , ,
 i
i 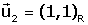 . .
Si P té coordenades  en referència R, quines són les seves coordenades
en referència R, quines són les seves coordenades
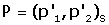 en referència S?
en referència S?
|
Solució.
Introduïm una referència auxiliar
 . Les coordenades de P
en referència T són (canvi d'origen): . Les coordenades de P
en referència T són (canvi d'origen): 
Efectuant ara un canvi d'eixos de T a S s'obté:

|
En general, si  i
i
 són les dues referències al pla i es coneixen les
coordenades en referència R dels vectors de S,
són les dues referències al pla i es coneixen les
coordenades en referència R dels vectors de S,  i
i  i de l'origen
i de l'origen  , llavors
, llavors

El procés descrit és del tot general, i serveix també per a referències amb 3 o més vectors (espai, ...)
El canvi invers (canvi de S a R).
Si es coneix les coordenades d'un punt en la nova referència S,
les coordenades en la referència original R s'obtenen fent:
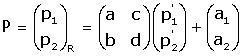
¿
 i
i
 on
on
 ,
,
 i
i 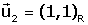 .
.
 en referència R, quines són les seves coordenades
en referència R, quines són les seves coordenades
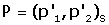 en referència S?
en referència S?
 . Les coordenades de P
en referència T són (canvi d'origen):
. Les coordenades de P
en referència T són (canvi d'origen): 

 a
a
 .
.
 i
i  i de l'origen
i de l'origen  , llavors
, llavors